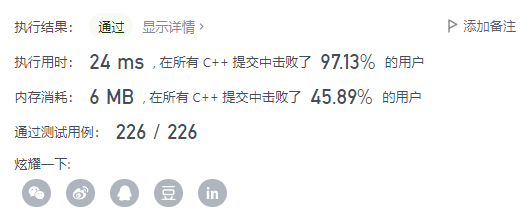
2002. Maximum Product of the Length of Two Palindromic Subsequences

Description

Solution

We could enumerate all the potential substring then check if they are palindromic by using state compression.

Then we iterate the subset of the inverse state to check if two substring are compatible.

Code

class Solution {
public:
    int maxProduct(string s) {
        int n = s.size();
        vector<bool> dp(1 << n);
        dp[0] = true;
        int res = 0;
        for(int i = 1; i < 1 << n; i++){
            auto [h,t] = getHT(i, n);
            if(h == t){
                dp[i] = true;
            }else{
                dp[i] = (s[h] == s[t]) && dp[i - (1 << h) - (1 << t)];
            }
        }
        for(int i = 1; i < (1 << n); i++){
            if(!dp[i])
                continue;
            int mask = (1<<n) -1 - i;
            int len = __builtin_popcount(i);
            for(int j = mask; j > 0; j = (j-1) & mask){
                if(dp[j]){
                    res = max(res, len * __builtin_popcount(j));
                }
            }
        }
        return res;
    }

    pair<int,int> getHT(int num, int n){
        int l = n, r = 0;
        while(true){
            if(num & (1<<l))
                break;
            l--;
        }
        while(true){
            if(num & (1 << r))
                break;
            r++;
        }
        return make_pair(l,r);
    }
};