1681. Minimum incompatibility

Description

image-20210904133436617

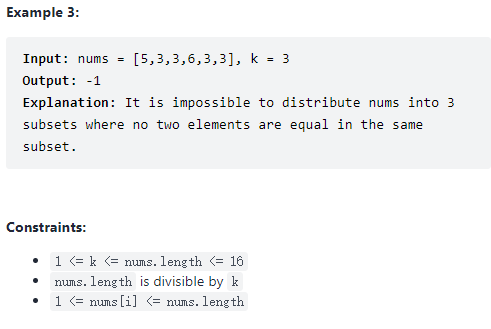
image-20210904133509355

Solution

We firstly compute the cost[i] , which i should be the mask of the elements in one set.

Then we compute dp[mask] , and the recurrence relation is :

1
dp[mask] = min(dp[mask ^ subset] + cost[subset])

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
    int minimumIncompatibility(vector<int>& nums, int k) {
        int n = nums.size();
        if(n % k) return -1;
        if(n == k) return 0;
        vector<int> cost((1 << n));
        vector<int> freq(n+1);
        for(int i = 0; i < 1 << n; i++){
            if(__builtin_popcount(i) != n /k)
                continue;
            fill(freq.begin(), freq.end(), 0);
            int flag = 1;
            for(int j = 0; j < n; j++){
                if(i & (1<<j)){
                    freq[nums[j]]++;
                    if(freq[nums[j]] > 1){
                        flag = 0;
                        break;
                    }
                }
            }
            if(flag){
                int l = 1, r = n;
                while(!freq[l])
                    l++;
                while(!freq[r])
                    r--;
                cost[i] = r-l;
            }
        }
        vector<int> dp((1 << n), 1E6);
        dp[0] = 0;
        for(int mask = 0; mask < 1 << n; mask++){
            if(__builtin_popcount(mask) %(n/k)) continue;
            //enum subset
            for(int subset = mask; subset > 0; subset = (subset-1)&mask){
                if(__builtin_popcount(subset) != n/k) continue;
                if(cost[subset]){
                    dp[mask] = min(dp[mask], dp[mask^subset] + cost[subset]);
                }
            }
        }
        return dp[(1 << n)-1] == 1E6 ? -1 : dp[(1 << n) -1];
    }
};

image-20210904134149578